Aswan CTF 2025 Finals

Introduction

Firstly, I'm happy to announce that I've participated in the finals of the first version of Aswan CTF 2025 and achieved 1st place with my team "وجه بحري boyz"

Unfortunately, I’m not in the photo because the ceremony was delayed and I had to leave early to catch the train 😢

This write up is for the second reverse engineering challenge mainly ( stay tuned for the 3rd one ), but I’ll give a quick walkthrough in the first challenge

First Challenge ( EAAS )

we are given a binary and a cipher CAS{Y6oduOh_X3_gQu3xn6t_EXF_J3vxhf_Ca_3yM7zln}

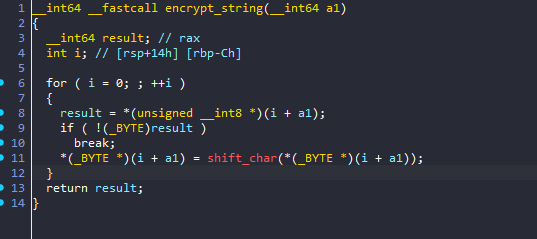
From the main function we can see that this program simply takes an input string and encrypts it in some way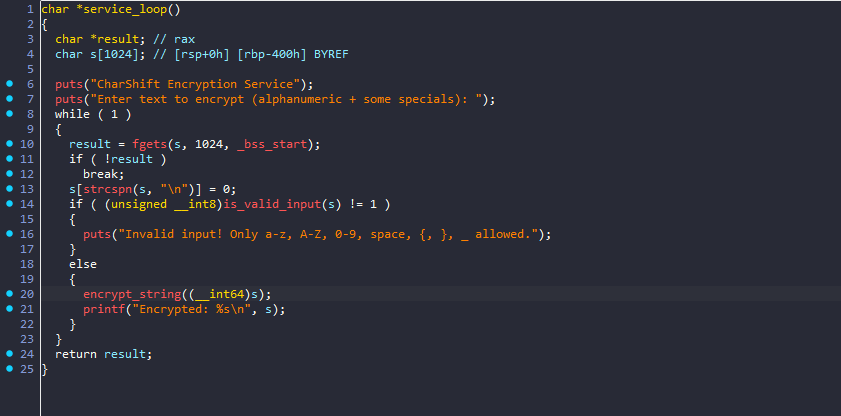

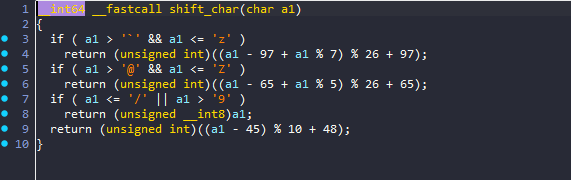
The encryption is simple

it takes each character and shifts it based on if it’s lower case, upper case, or a digit and left other characters untouched.

solving this can be done in many ways - I chose to simply brute force each character until I found the correct string that would produce the same cipher text

and here is the script

def decrypt_char(encrypted_c):
    e = ord(encrypted_c)
    if 'a' <= encrypted_c <= 'z':
        for original in range(ord('a'), ord('z') + 1):
            if (original - 97 + original % 7) % 26 + 97 == e:
                return chr(original)
    elif 'A' <= encrypted_c <= 'Z':
        for original in range(ord('A'), ord('Z') + 1):
            if (original - 65 + original % 5) % 26 + 65 == e:
                return chr(original)
    elif '0' <= encrypted_c <= '9':
        for original in range(ord('0'), ord('9') + 1):
            if (original - 45) % 10 + 48 == e:
                return chr(original)
    return encrypted_c if not encrypted_c.isalnum() else '?'

def decrypt_string(encrypted_text):
    return ''.join(decrypt_char(c) for c in encrypted_text)

enc = "CAS{Y6oduOh_X3_gQu3xn6t_EXF_J3vxhf_Ca_3yM7zln}"
print(decrypt_string(enc))

this will output: BAO{W3lcoMe_T0_aNo0th3r_CTF_H0sted_By_0xL4ugh}

a small tweak to match the flag format and here is the flag

YAO{W3lcoMe_T0_aNo0th3r_CTF_H0sted_By_0xL4ugh}

Second Challenge ( 3agamesta )

Introduction

For this challenge we are given a windows binary and a file named flag.png.encrypted

we can assume that this exe was used to encrypt the flag.png file

First look

just executing the exe. it will ask for an argument in usage

I opened the file in IDA and after some messing around, things were actually hard to identify. I couldn’t tell what the program was doing until I noticed some strings like .NET, .NETcore and dotnet. I suspected that this was a .NET program.

Even though Detect It Easy said that it’s a C/C++ compiled program and not a .NET program, that’s when I thought about .NET AOT.

That’s when we need to use a FLIRT signature file to rename some functions,

You can read more about FLIRT and .NET AOT in this article.

Getting Started

once I applied the signature things became more clear

I’m solving this challenge in a debugging session so functions names will be like 7FF..

Inside __managed__Main I go to sub_7FF7B0BA4930 which is the actual main function of the program

my signature file isn’t perfect so there will be still missing names.

anyways, after the program checks for the number of args, it will try to read the file that it was given as an argument.

then that sub_7FF7B0BA4A20 is where all the magic happens

sub_7FF7B0BA4A20

I’ll break down the function step by step

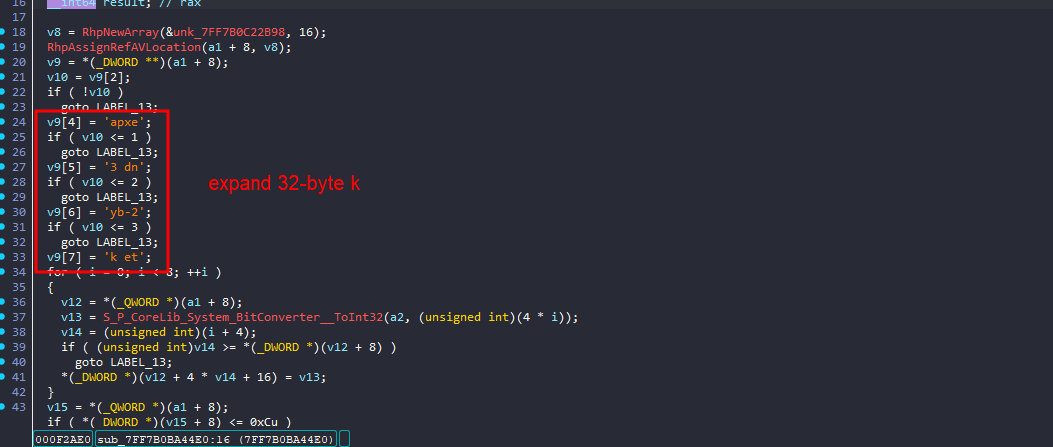
first interesting thing is this function

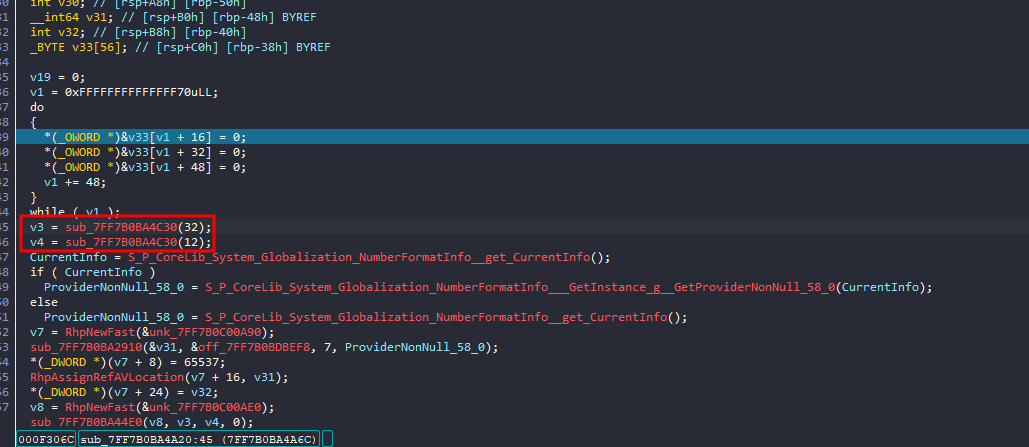
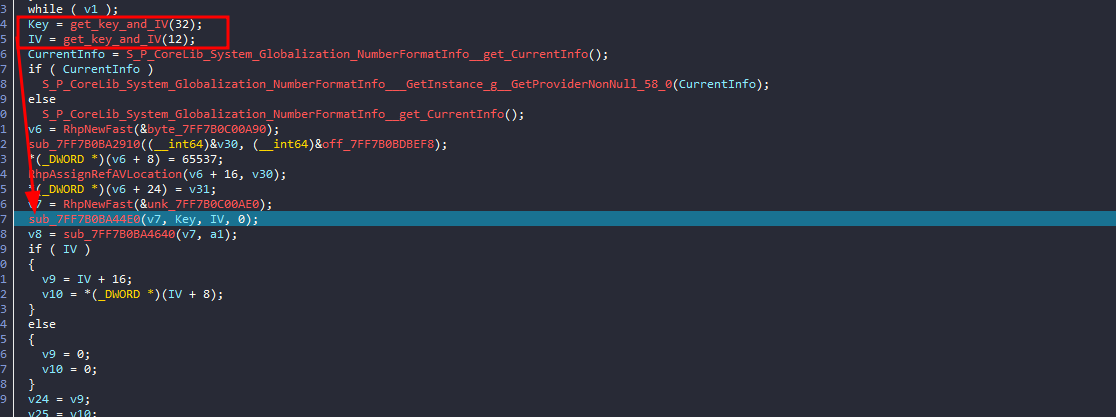
inside, it basically calls a RandomGeneration function, and it was called twice, so it will generate two random numbers, one with size of 32 and the other with size of 12 (pretty interesting lengths (can assume a key and IV but let’s make sure))

these 2 variables will be used in this function

and inside that function there is an interesting string

expand 32-byte k

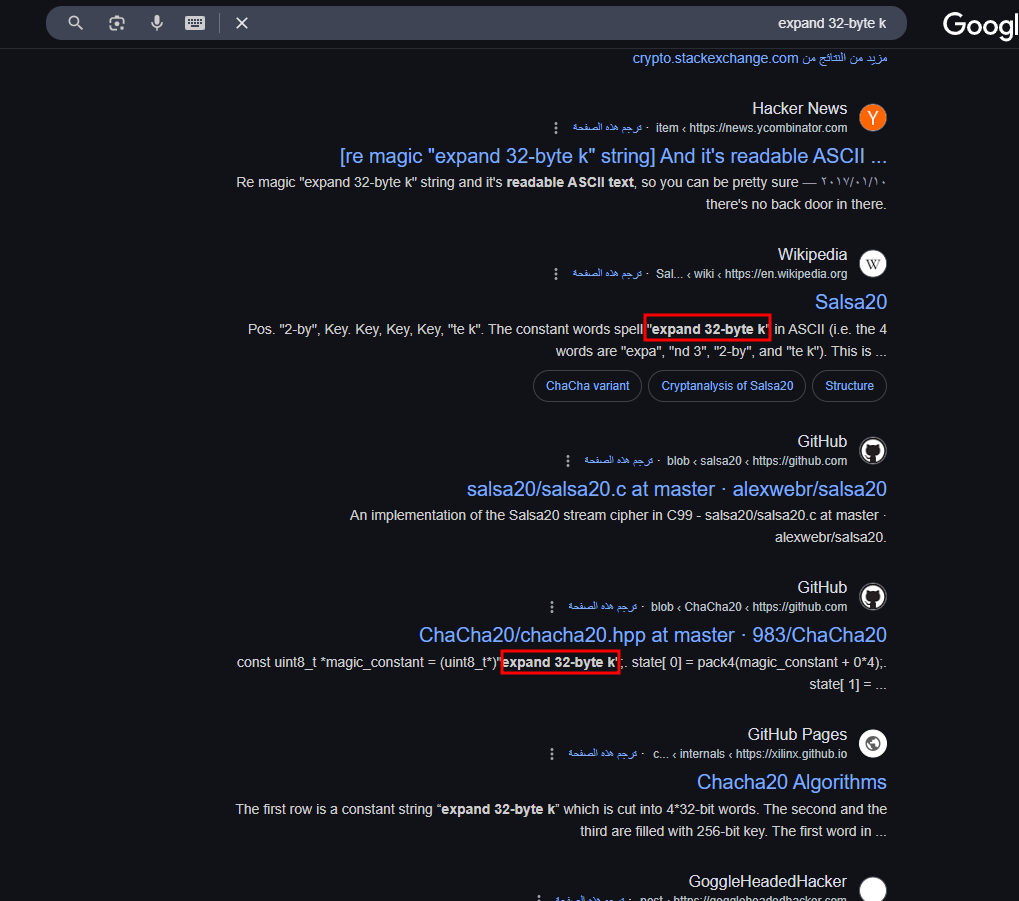
searching this string, it’s actually a strong indicator for a crypto algorithms called salsa20 or chacha20

this algorithm typically requires 16 or 32 byte key and 8 or 12 byte IV

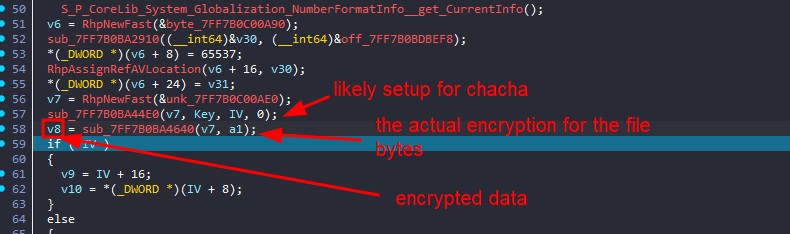
the next call should be the actual chacha20 encryption

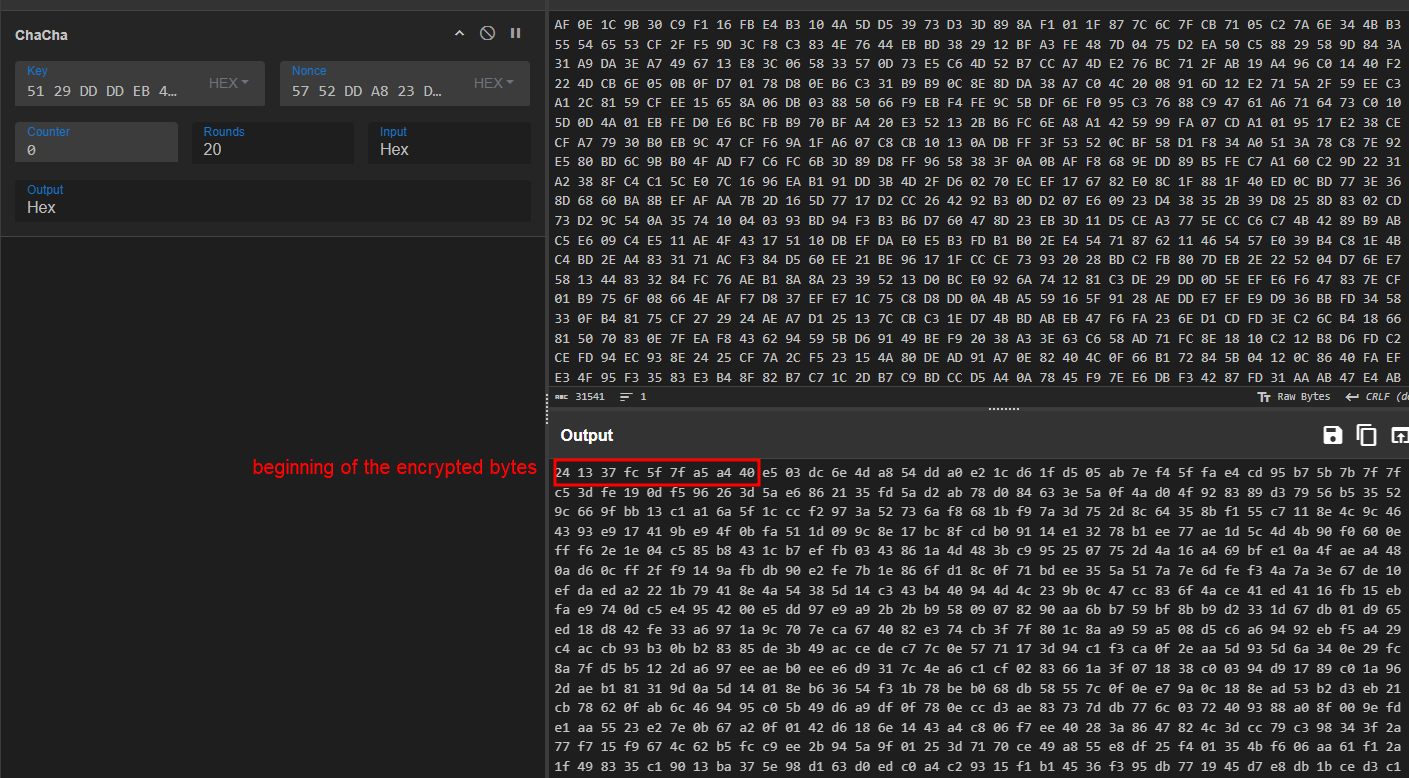
to confirm that, we will take the random generated key and IV in my debugging session, take the file into cyberchef and try to use the same key and IV for encryption and see if we will get the same result as the program

and the program output is the same

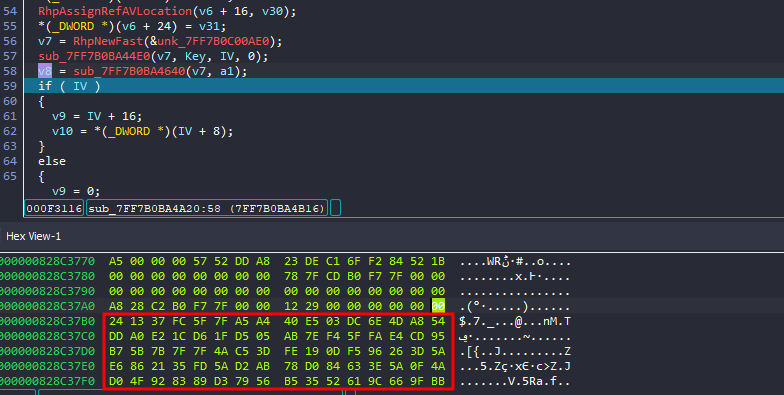
continue debugging, we see the IV value being passed from a variable to another and lastly being used in the function sub_7FF7B0BA1C70

this function is actually very big you can either assume what it does or ask AI :), if you choose the assumption route you can see it takes the IV as second arg, and the 3rd arg holds 0x10001 or 65537 which is pretty common value for e in RSA

but to encrypt something with RSA you need the public key which consist of 2 things

• n (the modulus): A large number that is the product of two prime numbers, p and q
• e (the exponent): A number that is relatively prime to (p−1)(q−1) and is used to encrypt the message.

and of course the plaintext that will be encrypted itself

so it looks like we missed the n, the 4th arg, let’s rewind a little bit

we can see we missed a function earlier that actually just assigns a static value for N to a variable

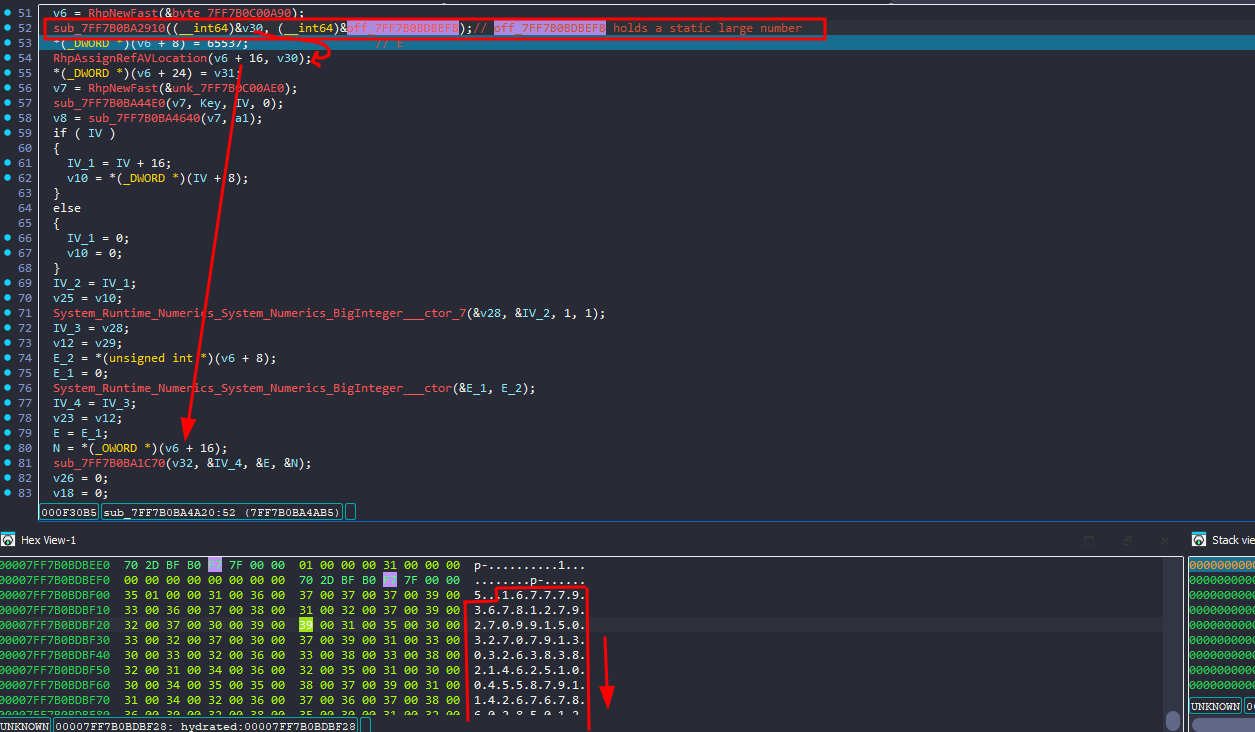RhpNewFast is a runtime helper function in .NET AOT for object allocation, and RhpAssignRefAVLocation is mostly related to array/vector memory management or allocation in .NET AOT too

asking AI about sub_7FF7B0BA1C70 will confirm that it’s RSA related and will be used for encryption

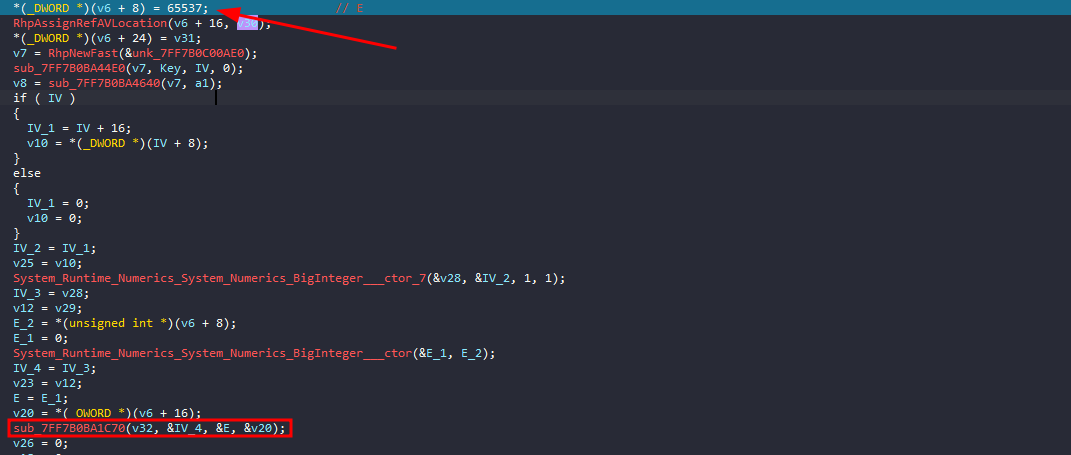
so the IV is now RSA encrypted

let’s move to the last part of the program, we see the encrypted IV being converted from large integers to a byte array in System_Runtime_Numerics_System_Numerics_BigInteger__TryGetBytes

and then there is one function that will be called twice

The first one takes 2 args, pointer to the encrypted file and the key The second one takes 2 args, pointer to the encrypted file and the encrypted IV

executing both and looking at results, we see it embeds both key and encrypted IV at the end of the encrypted file and that will be how we can actually solve this challenge!

Problem

now, we can get the original KEY and encrypted IV used to encrypt the flag.png file, but there is still a problem, the IV is RSA encrypted, without the private key we can’t decrypt it

what private key consists of is

• n (the modulus) The same modulus used in the public key.
• d (the private exponent) A number that is the modular multiplicative inverse of e modulo (p−1)(q−1)

in order to get the private exponent, we need to know the prime numbers p and q, but we can’t because we only have the modulus n

but let’s take a closer look on that n again maybe we can factorize it?

n = 167779367812792709915032707913032638382146251004558791142676786028501280044057627112826094280092505414510766384827088804978848108688648026981142540400168610823829003843442596437735093142183606826724002523744218048425313679193864739770021775952653310093258321014896182483000543295733022993925140727306455407233

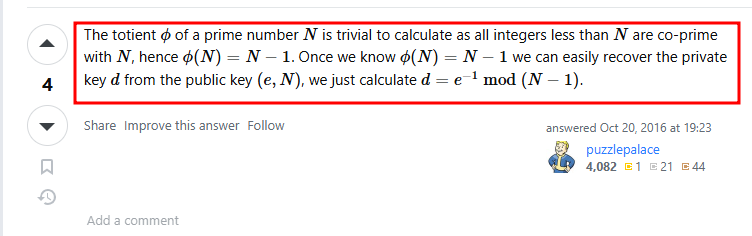
unknown factors but wait, the status is P (prime)

There can’t be a prime n

And this is actually a known wrong RSA implementation. With that info alone, we can calculate d as follows

Solution

n = 167779367812792709915032707913032638382146251004558791142676786028501280044057627112826094280092505414510766384827088804978848108688648026981142540400168610823829003843442596437735093142183606826724002523744218048425313679193864739770021775952653310093258321014896182483000543295733022993925140727306455407233
e = 65537

phi = n-1
d = pow(e, -1, phi)

print(d)

d = 34770883220674589713688057721208009132342194197841181337257367713491682340637970786676289920384155645511470299811122269088037520976077902596363550112380641045657346692732919493069838946810774797756464322100400835157431838363231012947746093977279052408359163770455161976961310085030531124456280595057391661825

Let’s get the IV from the encrypted file

decrypting that IV…

from Crypto.Util.number import  long_to_bytes

n = 167779367812792709915032707913032638382146251004558791142676786028501280044057627112826094280092505414510766384827088804978848108688648026981142540400168610823829003843442596437735093142183606826724002523744218048425313679193864739770021775952653310093258321014896182483000543295733022993925140727306455407233
e = 65537

# take all the bytes after the 32 bytes key and it will be the encrypted IV
cipher = bytes.fromhex("80 C0 EC CF FB CF 6D 35 69 AC 35 43 FD 5D 7F 8C F9 FD 7B E3 47 84 0F 51 61 A2 F9 27 89 0F C5 07 1D AD D4 36 DE BB 34 CF 6A 4B A1 36 28 D3 F3 B6 43 41 86 C1 A8 55 FB 60 10 5B EB C3 04 B3 DD 33 C1 4D 4C E7 64 61 C4 D7 DB 7F 06 01 2A 17 F2 DE 00 51 45 59 37 08 1D AD 97 4E 99 71 12 DB BA 64 DB 27 71 2E 7B E6 29 81 9F 44 8D 92 6F 21 C5 05 52 C9 CC B9 FE EC 34 46 9B 5E 6A 1D 1C F5 CB 51")
#print(cipher)

c = int.from_bytes(cipher, 'little') # little endian because of how `System_Runtime_Numerics_System_Numerics_BigInteger__TryGetBytes` actually works

phi = n - 1  

d = pow(e, -1, phi)

m = pow(c, d, n)

print(hex(int.from_bytes(long_to_bytes(m)))[2:])

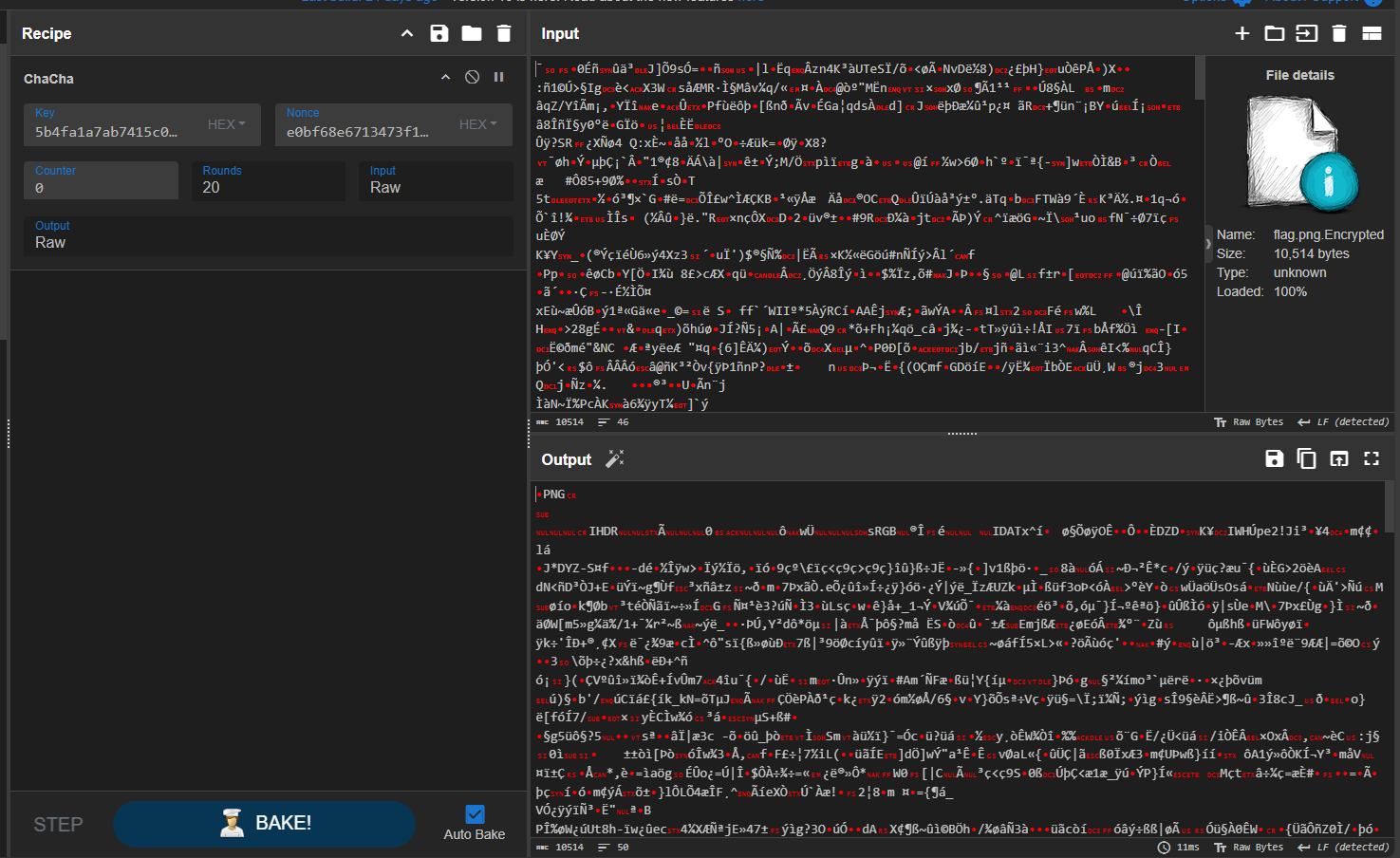
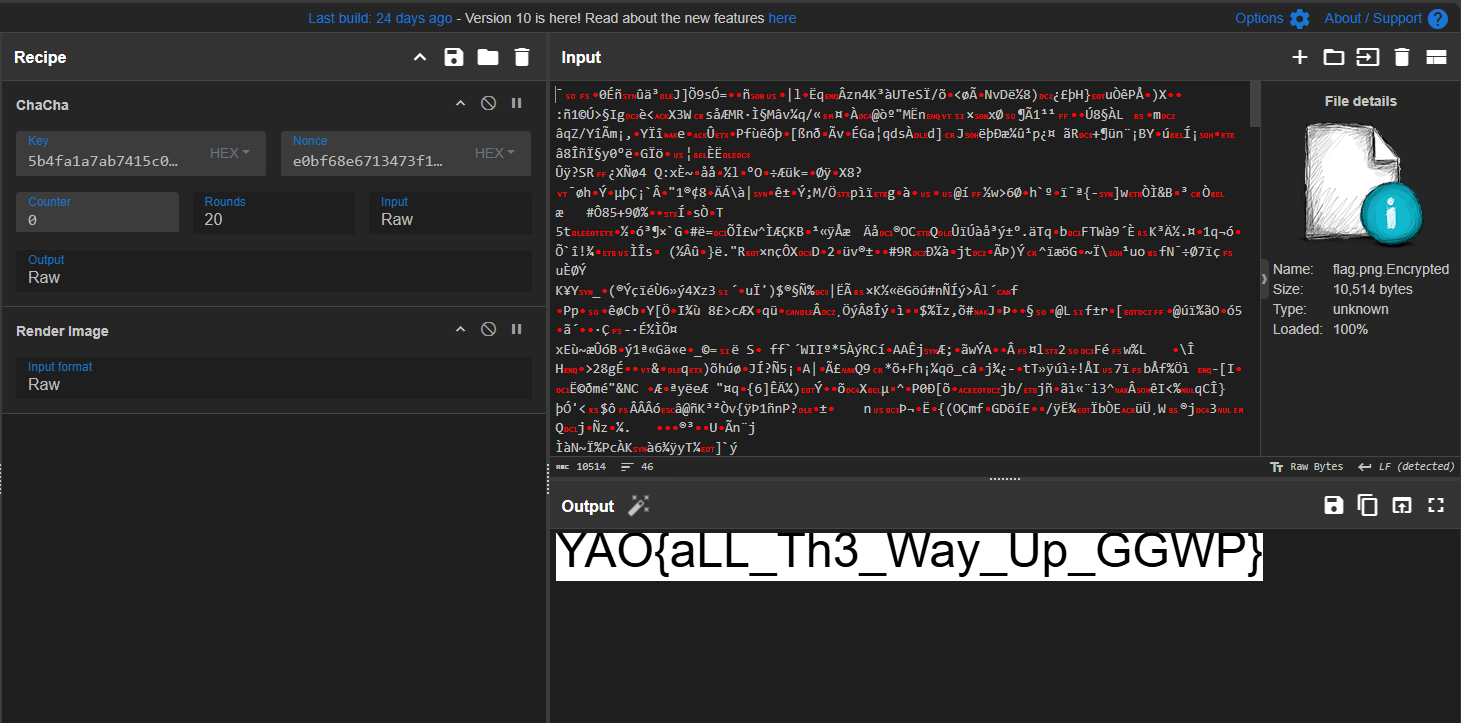
IV = e0bf68e6713473f1bf3b488f KEY = 5b4fa1a7ab7415c0cba40be0521a9bf5949bea22eb1fc72a05a92f6fa42d7718

Flag time

let’s decrypt in cyberchef

and we got the flag! YAO{aLL_Th3_Way_Up_GGWP}

Third Challenge ( monolith )

Stay tuned

Last words

Thank you for reading, and I hope you found it helpful.

If you have any questions or comments, feel free to contact me on LinkedIn — Discord — GitHub

Also, you can check my other blog where I post some cool DFIR CTF write-ups too from time to time